기회가 있어서 퍼즐위치사가를 클론하게 되었는데, 내용 구조 상 오리지널 게임 퍼즐보불이랑 유사한 점이 많았다. 이제 단순히 만드는 것도 만드는건데, 만들기 전에 코드를 사전에 어느정도 생각하고 접근하면 좋겠다고 생각했다. 이번에 만들기까지의 생각이 워낙 많았기에 풀어보고자 한다.
https://play.google.com/store/apps/details?id=com.king.bubblewitch3&pcampaignid=web_share
버블위치사가3 - Google Play 앱
버블위치사가3 - 완전히 새로운 버블 슈팅 게임!
play.google.com
요구사항 정의하기
게임이 퍼즐보블에서 보다 다채로운 내용들이 추가된 편이다. 나는 스테이지에 있는 내용들을 제거하는 것 뿐만 아니라 조건과 특수한 상황이 어느정도 갖추어져있는 한 특수 스테이지를 클론하기로 했다.
우선, 결정 후에는 해당 게임을 플레이하면서 요구사항을 간략히 정리했다. 녹화해둔걸 여러 번 돌려보면서 클론에 대한 기획을 했다. 스테이지를 클론하는 것이지만 스테이지는 결국 게임 상에서 구성되는 내용이기때문에 준비해야 할 기저가 정말 많았다.
퍼즐보블의 기초인 3개의 같은 색 오브젝트가 인접하면 제거된다, 인접한게 없으면 즉시 제거한다. 등 룰만 생각하고 접근하기엔 생각할게 많았고 왠만하면 하루에 모든 내용이 나오길 바랬다 (나중에 보니 마감직전에 가서 또 발견했다)
이 과정에서 선택해야 했던 것은 좌표체계였다. 내가 리서치한 것과 기존의 사람들이 클론 해둔 것들부터 방향이 갈렸다. 게임을 보면, 한 버블을 중심으로 6방향으로 버블이 감싸질 수 있다. 즉, 스테이지 상에서는 육각 좌표계를 사용하는 것이다. 통상적인 3차원 값들을 전환해야 할 계산식이 필요한 상황이었다.
Axial Coordinate
다소 학습곡선이 있다고 느껴졌지만 이후 코드가 직관적이 되고, 무엇보다 BFS로 문제를 풀 때 dx, dy를 쓰듯 전개 할 수 있다는 점에서 괜찮은 선택지라 생각했다.
Offset Coordinate
못쓸것은 아니지만, 이 방법은 내 위치가 몇 번쨰 칸에 있냐에 따라 보정값이 들어가기 때문에 이름에 Offset 이 들어갔다. 만드는 것 자체는 보다 간단 할 수 있다지만 후 관리와 코드 가독성에 신경이 많이 갈 수 있다는 점이 내키지 않았다.
코드식 전환
앞 내용부터 편파적이지만 Axial Coordinate 형식으로 결정했다. 이 방법은 일정 범위 내의 3차원 식을 모두 q, r 이라는 일관된 별도 좌표 체계로 전환하여 사용한다. 물론 그 역도 가능하다. 변환식을 사전에 만들어놓고 활용처가 있을 때마다 꺼내서 쓸 생각이었다.
물론 일정 범위 내의 [x y z]가 [q r]로 전환 된 후 [q r]에서 [x y z]로 전환되면 변환 전의 값으로 그대로 반영되진 못한다. 그 언저리를 다 한 위치로 묶는데 의의가 있음. 진짜 필요한 부분에 변환식을 적용하는게 맞다.
World To Hex : x, y를 받아 q, r로 변환
public static Vector2Int WorldToHex(Vector2 worldPos)
{
float r_f = (2.0f / 3.0f * worldPos.y) / hexCellRadius;
float q_f = (worldPos.x / (hexCellRadius * Mathf.Sqrt(3.0f))) - (r_f / 2.0f);
return AxialRound(q_f, r_f);
}AxialRound를 반올림 식으로 던지는 내용인데 아래 내용에서 마저 논하도록 하겠다.
먼저 코드에 직접적으로 때려버린 루트3 과 3분의 2가 어디서 왔는지를 확실히 하고 가자.
이 식은 육각형 생김새가 위아래쪽이 뾰족한, 용어로는 Pointy-top 형태를 나타낸다.
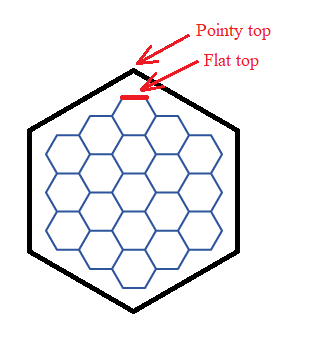
hexCellRadius은 육각형 중심에서 꼭지점 가지의 거리를 가리킨다.
private static Vector2Int AxialRound(float q, float r)
{
float x = q;
float z = r;
float y = -x - z;
Vector3 roundedCube = CubeRound(x, y, z);
return new Vector2Int((int)roundedCube.x, (int)roundedCube.z);
}
private static Vector3 CubeRound(float x, float y, float z)
{
int rx = Mathf.RoundToInt(x);
int ry = Mathf.RoundToInt(y);
int rz = Mathf.RoundToInt(z);
float dx = Mathf.Abs(rx - x);
float dy = Mathf.Abs(ry - y);
float dz = Mathf.Abs(rz - z);
if (dx > dy && dx > dz) rx = -ry - rz;
else if (dy > dz) ry = -rx - rz;
else rz = -rx - ry;
return new Vector3(rx, ry, rz);
}아래의 역연산 과정보다 첫 변환 과정이 좀 내용이 많은 이유는 반올림에 관한 문제이다. 여기서 만들어진 q, r을 냅다 반올림을 때려버렸다간 경계 지점에서 실제 위치랑은 하나도 상관없는 엉뚱한 타일을 선택할 여지가 생긴다. 정확한 타일을 찾기 위한 보정 작업인 것이다.
AxialRound함수에서 x + y + z = 0라는 식에 관한 값을 지정해준 뒤, 그 이후에 CubeRound 에서 실질적인 반올림을 수행한다. 여기서 앞에 설명했던 범위 이내가 다 한 부류의 q, r 로 묶이는 이유가 설명 된다.
- 우선 반올림을 모두 때린 다음 기존 값이랑 빼봤을 때(dx dy dz) 오차가 있는 값을 찾는다. 가장 오차가 크다면, 반올림에서 일명 "찐빠"가 났을 확률이 제일 높다는 것이다.
- 그 값을 1순위로 버리고, 앞에서 논했던 x + y + z = 0 식에 기반해 재 계산을 진행한다. 이로써, 가장 가까운 타일의 큐브 좌표 정의가 가능해진다.
Hex To World : q, r을 받아 x, y로 변환
public static Vector2 HexToWorld(Vector2Int hexCoords)
{
float x = hexCellRadius * Mathf.Sqrt(3.0f) * (hexCoords.x + hexCoords.y / 2.0f);
float y = hexCellRadius * (3.0f / 2.0f * hexCoords.y);
return new Vector2(x, y);
}앞에 개고생을 해둬 만들어준 q, r 좌표를 역연산으로 간단하게 끝난다.
진짜 필요한 이야기는 다 했다. 이제 이렇게 기저를 만들어두면 주변 순회를 이런 함수 한 개로 가능해진다. 이 부분은 이후에 구현 하면서 다시 언급할 것이다.
private static readonly Vector2Int[] neighborDirections = new Vector2Int[6]
{
new Vector2Int(1, 0), new Vector2Int(-1, 0),
new Vector2Int(0, 1), new Vector2Int(0, -1),
new Vector2Int(-1, 1), new Vector2Int(1, -1)
};
public static List<Vector2Int> GetNeighbors(Vector2Int hexCoords)
{
List<Vector2Int> neighbors = new List<Vector2Int>();
foreach (var direction in neighborDirections)
{
neighbors.Add(hexCoords + direction);
}
return neighbors;
}
'구현하기 > Unity' 카테고리의 다른 글
| 트러블슈팅 : WayPoints에 못닿는 문제 (0) | 2025.10.23 |
|---|---|
| 경매 시스템 구현 #2 (0) | 2025.10.20 |
| 경매 시스템 구현 #1 (0) | 2025.10.19 |
| 퍼즐위치사가 3 클론 #3 : 경로 개념과 레벨 디자인 (1) | 2025.10.03 |
| 퍼즐위치사가 3 클론 기록 #2 : MVP 만들기 (1) | 2025.09.26 |
